目录
什么是完美气体?
完美气体或理想气体是一种物质的状态,它从液态蒸发完成,在任何压力和温度条件下都严格遵守所有气体定律。在现实中,不存在在所有压力和温度条件下都遵守所有气体定律的理想气体或完美气体。而普通的氧、氢、氮、空气等真实气体则难以液化;在一定的压力和温度范围内,可以认为是理想气体(或理想气体)。
气体的物理性质由三个变量控制,这三个变量是
- 气体施加的压力,
- 气体所占的体积
- 气体的温度。
完美气体的行为可以用下列从实验结果中证明的气体定律来研究。
- 波义耳氏定律
- 查理定律
- 吕萨克定律
让我们详细讨论气体的这些定律
波义耳氏定律
这条法律是罗伯特·波义耳在1662年制定的。
声明:
它指出,在温度恒定的情况下,一定质量的完美气体的绝对压强与其体积成反比。
在数学上

后缀1、2和3…表示不同的条件集。
解释:
为了理解这个定律,让我们做一个实验。

假设我们有一个气缸活塞组件,其中包含一种气体。保持这个系统在室温下(所以温度保持不变),如果我们通过施加一个比钢瓶内气体压力增加的外力来减小体积。如果外部负荷被移除气体的体积就会开始增加压力就会降低。这证明了当完美气体的压强比体积增大时,它的体积会减小,当体积减小时,压强会增大。
查理定律
这项法律是在1787年由法国人雅克·c·查尔斯颁布的。
声明
这条定律可以用两种方式表述
声明1
在恒定的绝对压强下,一定质量的完美气体的体积与它的温度成正比。
解释:

让我们再次采取活塞缸总成是保持在室温。活塞的上部暴露在大气压力下(因此系统保持恒定的绝对压力)。圆柱体的下部是热导体。现在加热圆筒底部。过了一段时间,气缸的活塞开始向上运动。为什么会发生这种情况?你能猜到吗?让我告诉你实际发生了什么。当气缸被加热时,气缸内的气体温度升高,压力也增加,使气体膨胀,对活塞施加一个力,使活塞向上运动。活塞向上运动以保持压力恒定(即气体的内部压力等于大气压力)。 The upward movement of the piston increases the volume of the gas
因此,我们可以得出这样的结论:当系统的绝对压强恒定时,此时气体的体积与温度成正比。
在数学上

语句2
在恒定压强下,所有的完备气体在0摄氏度时,温度每改变1摄氏度,其体积就会改变原来体积的1/273。
让
什么是绝对零度?
因为在0℃时,温度每降低一度,气体的体积就减少原来体积的1/273。所以如果我们把温度调到-273℃,那么气体的体积就会减少到0。
气体体积等于零的温度叫做绝对零度温度。
吕萨克定律
这条定律是约瑟夫·路易斯·吕萨克在1809年提出的。
声明
在体积恒定的情况下,一定质量的完美气体的绝对压强与绝对温度成正比。
在数学上

其中,后缀1、2和3…表示不同的条件集。
解释:

让我们以一个活塞缸总成为例,里面有理想气体。活塞是不动的。由于活塞是固定的,所以体积是恒定的。现在给圆柱体中的气体加热。气体的温度开始升高,气体的压力也随之增加。压力的增加可以从系统上的压力表上看到。
上述实验证明,在体积不变的情况下,完美气体的压强与它的温度成正比。
4.阿伏伽德罗定律
阿伏伽德罗定律有时也被称为阿伏伽德罗假设或阿伏伽德罗原理。这是由阿伏伽德罗在1811年提出的一个实验定律。
声明:
在恒定的温度和压力下,所有等体积的气体所含的分子数目相等。
或
对于一定质量的理想气体,在温度和压力不变的情况下,气体的体积与气体的物质量(摩尔数)成正比。
在数学上
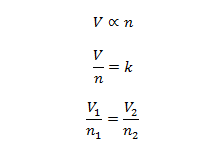
后缀1,2表示一种气体的不同条件集。
在哪里
V =气体的体积。
N =气体的物质量(单位:摩尔)。
k =常数,等于RT/P,其中R是通用气体常数,T是开尔文温度,P是压强。因为温度和压力是恒定的,所以RT/P也是恒定的,用k表示。
5.一般气体方程或理想气体定律
理想气体定律或一般气体方程是玻伊尔定律、查尔斯定律和阿伏伽德罗定律的组合形式。理想气体方程可以写成

在哪里
ρ =气体的密度= m/V
P =气体的压强
V =气体的体积
n =气体物质的数量(单位:摩尔)
R=理想,或通用气体常数
T =气体的绝对温度
以下是三种气体定律(即波义耳定律、查尔斯定律和吕萨克定律)的概述:

如果你觉得理解这些气体定律有什么困难,你可以通过评论来问我你的问题。如果你觉得这个话题很有用,那就把它分享给其他人。